With two points on a straight line, you can find the equation of a line.
Calculate the gradient from the two coordinates (use `frac(up)(along)`, or the formula `m=(y_2-y_1)(x_2-x_1)` where `(x_1, y_1)` and `(x_2, y_2)` are the coordinates). This gives a value for the gradient, `m`.
Substitute the value for `m`, and the values from one of the coordinates (it does not matter which one) into `y = mx + c` to obtain a value for `c`.
Substitute `m` and `c` into `y=mx+c` for the equation of the line.
Determine the equation of the linear function shown below.
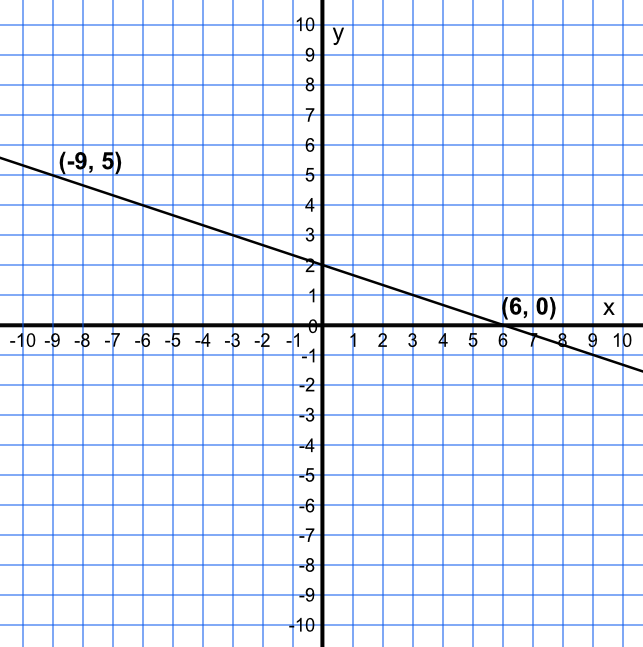
The difference between two points gives the gradient = `frac("difference in y")("difference in x")` = `frac((0 - 5))((6 - -9))` = `frac(-1)(3)`
`y = frac(-1)(3)x + c`
Substitute for one point, say (6, 0)
`0 = frac(-6)(3) - c`
`c = 2`
Check with other point (-9, 5): `5 = frac(-1)(3)xx-9 + 2` ✔
Answer: `y = frac(1)(3)x + 7`
There are three points (13, 5), (33, 10) and (299, 77). Are these points collinear (all on the same line)?
Work out the gradient using the first two coordinates:
`m = frac(33-13)(10-5) = frac(20)(5) = 4`
Substituting (5, 13) into `y=mx+c`:
`13=4xx5-c` gives `c=-7`
Check with (10, 33): `33=4xx10-7`✔
If (299, 77) is on the line then it would have to fit into the equation:
`299 ≠ 4xx77 - 7` therefore not on the line.
Answer: No. The first two points are on the line `y = 4x - 7`, and the third is not.