Parallel lines have the same gradient, or slope, but different intercept points on the `y`-axis. If both lines are written in the form `y=mx+c`, then the value of `m`, the gradient, will be the same for both lines.
A set of collinear points all exist on the same line.
Is the line defined by two points, (-5,-2) and (5,4), parallel to the line given by the equation `y = frac(3)(5)x - 3`?
Both gradients are the same, so the lines are parallel.
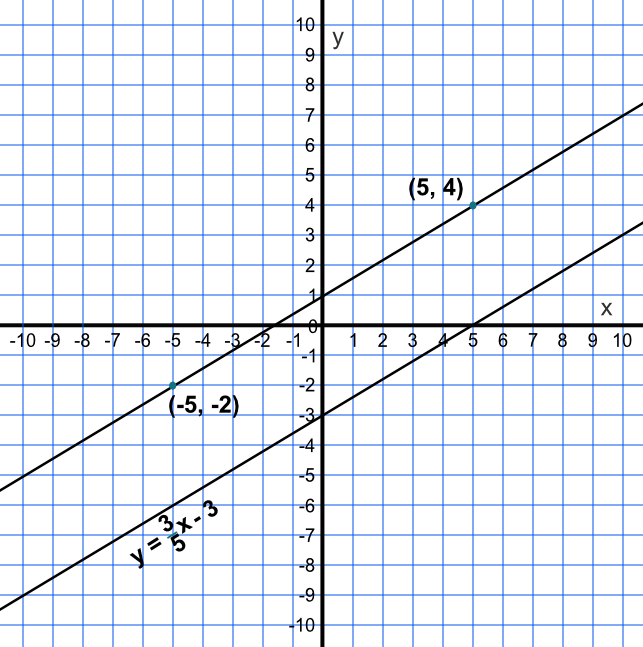
Answer: Yes. The gradient between these points is `frac(up)(along)` = `frac(4 - -2)(5 - -5)` = `frac(6)(10)` = `frac(3)(5)`.
A line is given by an equation `y = -2x + 4`. Give the equation of a line, parallel to the given equation, that passes through (0, 5).
The gradient is the same in both equations. Substitute the point into the equation:
`5 = -2xx0 + c` therefore `c=5`
The equation of the line is `y = -2x + 5`
Answer: `y = -2x + 5`