Perpendicular lines exist at right angles to each other.
Lines are perpendicular if the gradients of the two lines multiplied together = -1.
What is the equation of the line that is perpendicular to `y = 3x -3` and also passes through (0, 5)?
The gradient of the original line is 3. The gradient of the perpendicular line = - `frac(1)(3)` (reciprocal of the original gradient multiplied by -1).
The line passes through (0, 5), which is the intercept value, `c`.
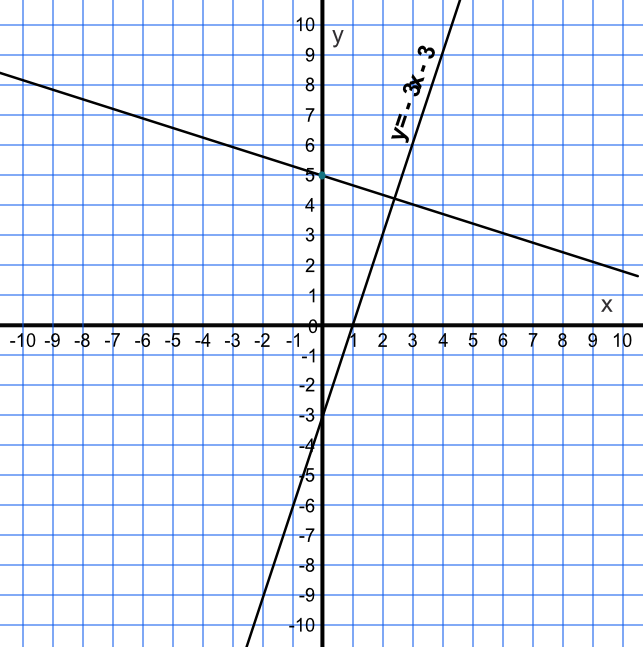
Answer: y = -`frac(1)(3)`x + 5
Find the equation of the line perpendicular to `y = frac(1)(2)x - 3` that passes through (4, 4).
The gradient of the second line is given by - 1 / `frac(1)(2)` = -2
The lines passes through the point (4, 4): 4 = -2 x 4 + `c`, where c is the intercept = 12
The equation of the line is `y = -2x + 12`
Answer: `y = -2x + 12`