Finding the factors of a number is called factorising. In addition to the numbers 1 and itself, factors of a number can often be factorised themselves.
Any number can be factorised into a set of prime numbers: this is known as the Product of the Prime Factors, or the Product of its Primes (Product is another word for multiplication). The number 24
• can be written as 4 x 6,
• which can then be written as (2 x 2) x (2 x 3).
The Product of the Prime Factors for 24 is 23 x 3.
A Prime Factor Tree can be used to obtain the Product of its Primes for a number. Start with the number. Create a pair of branches: at the end of each branch, enter any pair of factors for the number. Repeat the process for each branch unless it ends in a prime number. Multiply together the primes at the end of each branch.

90 = 2 x 5 x 3 x 3, re-arrange to:
90 = 2 x 3 x 3 x 5, re-write as powers
90 = 2 x 32 x 5
Every number greater than 1 is either a prime number or can be represented as the product of its primes. A number will always factorize to the same set of primes, and that set of primes cannot be multiplied together for any different number (the Unique Factorization Theorem).
Write 48 as the product of its primes.
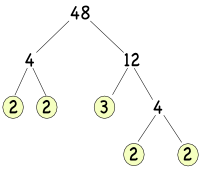
Answer: 48 = 24 x 3.
Write 144 as the product of its primes.
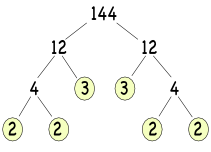
Answer: 144 = 24 x 32
See also Squares and Integer Powers and Roots