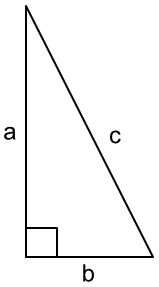
Pythagoras` Theorem states that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares on the other two sides.
Measure the length of each side, and then square each measurement. Add the squares of the two shorter sides together, and this will equal the square of the longest side.
The formula for this is `a^2 + b^2 = c^2`, where `c` is the longest side, or hypotenuse. It does not matter which the shorter sides `a` and `b` represent.
An elevation identifies an object above an observer. The elevation of this object forms a triangle joining the observer, the object, and a point on the ground immediately below the object. This is a right angle triangle. Depression is the same as elevation, except that depression has the object below the observer.
What is the length of the side `c` in this triangle? Give your answer to 1 decimal place.
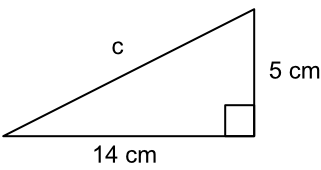
| Pythagoras` Theorem | `a^2 + b^2` | `= c^2` |
| Substitute | `(5)^2 + (14)^2` | `= c^2` |
| `25 + 196` | `= c^2` | |
| `221` | `= c^2` | |
| root both sides | `14.866` | `= c` |
| 1 decimal place | `14.9` | `= c` |
Answer: 14.9 cm
What is the length of the side CB in the triangle, below? Give your answer to three significant figures.
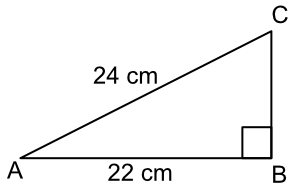
| Pythagoras` Theorem | `a^2 + b^2` | `= c^2` |
| Substitute | `(22)^2 + b^2` | `= (24)^2` |
| `484 + b^2` | `= 576` | |
| Subtract 484 both sides | `b^2` | `= 92` |
| root both sides | `b` | `= 9.59166` |
| to 3 sf | `b` | `= 9.59` |
Answer: 9.59 cm