GCSE(F) GCSE(H)
A quadratic function will contain a squared term, but will have no higher power. It will be in the shape of a parabola which is a curve that comes to a rounded point then turns to curve back again. The point at which it turns is a turning point, and this will be either a minimum or a maximum value.
It is necessary, when plotting quadratic graphs, to plot more than three points to establish the shape of the graph. The graph y = x2 - 3 may be plotted using the following points:
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| x2 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
| x2 - 3 | 13 | 6 | 1 | -2 | -3 | -2 | 1 | 6 | 13 |
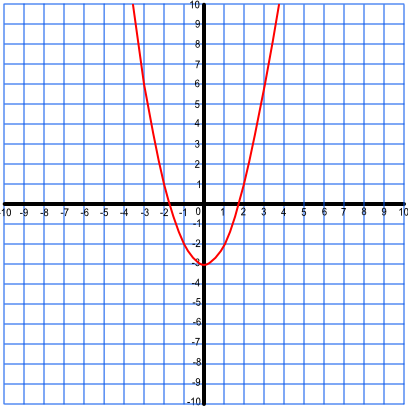
The turning point for this graph is at (0, -3). The roots of the function are found when y = 0: in this instance there are two roots at -1.67 and +1.67 (to 2dp). For any quadratic there may be two roots, one root (actually the same root repeated), or no roots (the graph does not cross y = 0.
Exam Tip: draw graphs as accurately to obtain any turning points or roots.
1. Plot the graph for y = 2x2 -6
Answer: 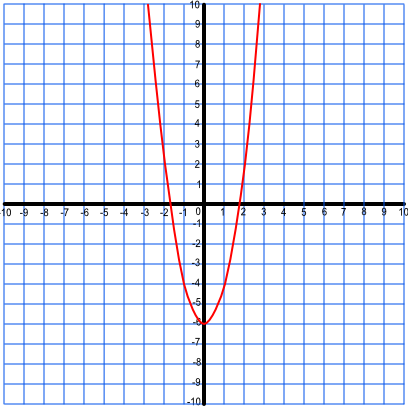
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| 2x2 | 32 | 18 | 8 | 2 | 0 | 2 | 8 | 18 | 32 |
| 2x2 - 6 | 26 | 12 | 2 | -4 | -6 | -4 | 2 | 12 | 26 |
2. What are the roots fory = x2 - 5x + 6?
Answer: 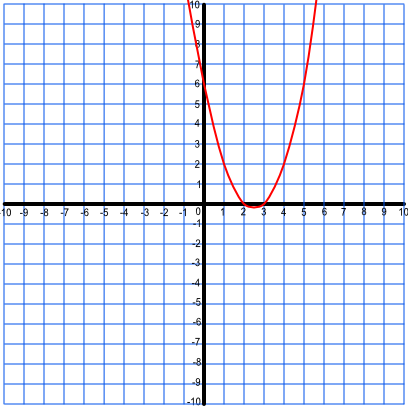
(2, 0) and (3, 0)
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| x2 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 |
| 5x | -20 | -15 | -10 | -5 | 0 | 5 | 10 | 15 | 20 |
| x2 - 5x + 6 | 42 | 28 | 20 | 12 | 6 | 2 | 0 | 0 | 2 |