There are a number of types of Transformation that can change the position and size of a shape.
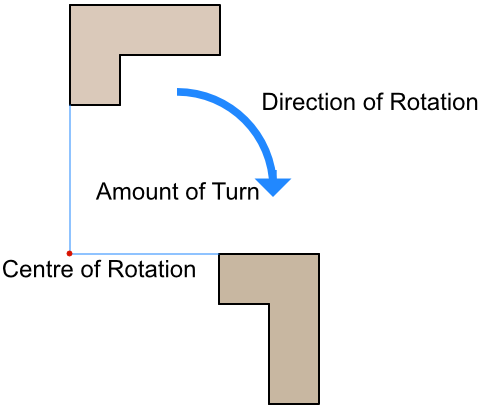
A shape is rotated by turning it. To fully describe a rotation, the following information is required:
the centre of rotation; the shape is turned around that point;
the amount of turn, which might be in degrees or given as a fraction;
the direction of rotation, which will be either clockwise or anticlockwise.
A rotation is only fully described if all three pieces of information are given (if a rotation is 180º, or a half-turn, the direction is not required as it does not matter in which direction the shape is rotated). Note that a rotated shape is congruent to the original shape.
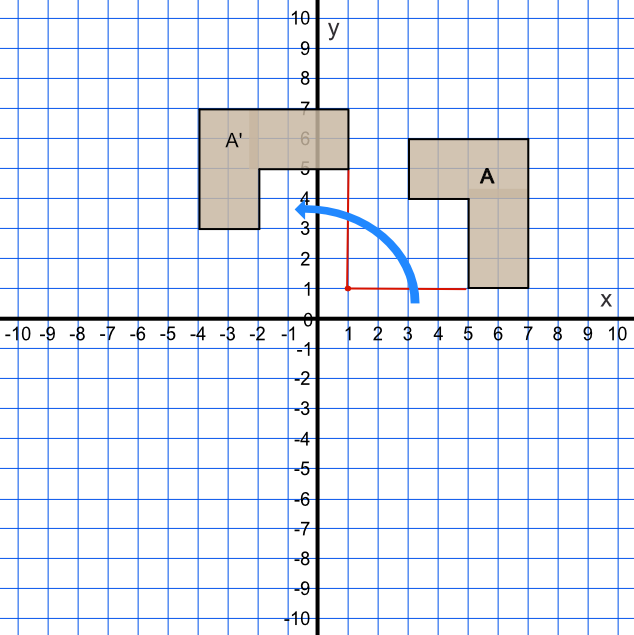
Rotate the shape A 90º anticlockwise, with a centre of rotation at (1, 1).

The best way to rotate a shape is to use tracing paper.
Draw the shape on the tracing paper. Rotate the point about (1, 1) by using a sharp point (eg the end of a compass). Rotate the tracing paper anticlockwise by a quarter turn (90º). Mark the new points of the shape.
Answer:
Describe fully the transformation that moves shape A onto shape B.

The shape has been turned.
To fully describe a rotation, you need the centre of rotation, the amount of turn, and the turn direction.
Because the shape is turned 180º, it does not matter whether the shape is rotated clockwise or anticlockwise and you can leave the direction of rotation out.
Answer: The transformation is a rotation.
It is rotated 180º.
The centre of rotation is (0, 0)