Sine Rule

The sine rule can be used for any triangle, whether right angles or not. Note that the letters relating to the side are opposite the corresponding letters for the angles, i.e. a and A; b and B and c and C.

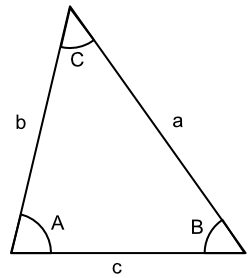
Relationship of sine rule

The rule is:

`frac(a)(sin A) = frac(b)(sin B) = frac(c)(sin C)`

Use the sine rule when any two sides and an angle, or two angles and a side are known, the sine rule can be used. The rule covers all three sides and all three angles, but normally you would only use two of the pairs.

The sine rule can also be used with the angles on top: `frac(sin A)(a) = frac(sin B)(b) = frac(sin C)(c)`

Example 1

What is the value of the angle `x`? Give your answer to 1 decimal place.

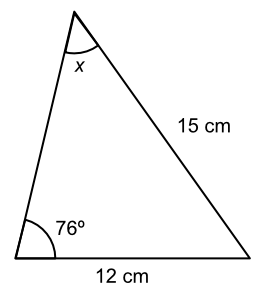
Find an angle with the sine rule

use the SIN rule	`frac(sin A)(a)`	`= frac(sin B)(b)`
substitute	`frac(sinA)(12)`	`= frac(sin 76)(15)`
x12 both sides	`sin A`	`=frac(12 xx sin 76)(15)`
	`sin A`	`=0.776`
sin^-1 both sides	`A`	`= sin^-1 0.776`
	`A`	`= 50.917`
to 1dp	`A`	`= 50.9`

Answer: 50.92º

Example 2

How long is the side x? Give your answer to 1 decimal place.

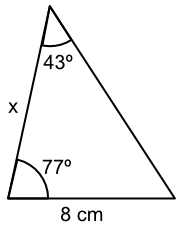
Find a length with the sine rule

The unknown length is opposite an unknown angle.

unknown angle	`180 - 77 - 43`	`=60`
use the SIN rule	`frac(sin A)(a)`	`= frac(sin B)(b)`
substitute	`frac(x)(sin 60)`	`= frac(8)(sin 43)`
	`x`	`= frac(sin 60 xx 8)(sin 43)`
	`x`	`= 10.159`
to 1 dp	`x`	`= 10.2`

Answer: 10.2 cm