Graphs can be stretched horizontally and vertically by applying scale factors. If the factor is applied before the function is evaluated, then the stretching takes place parallel to the x-axis, but the amount of stretching is a reciprocal of the factor:
Mapping `f(x)` onto `f(ax)` stretches a graph by factor `frac(1)(a)` on the x-axis.
If the factor is applied after the function is evaluated, then the stretching takes place parallel to the y-axis:
Mapping `f(x)` onto `af(x)` stretches a graph by factor a on the y-axis.
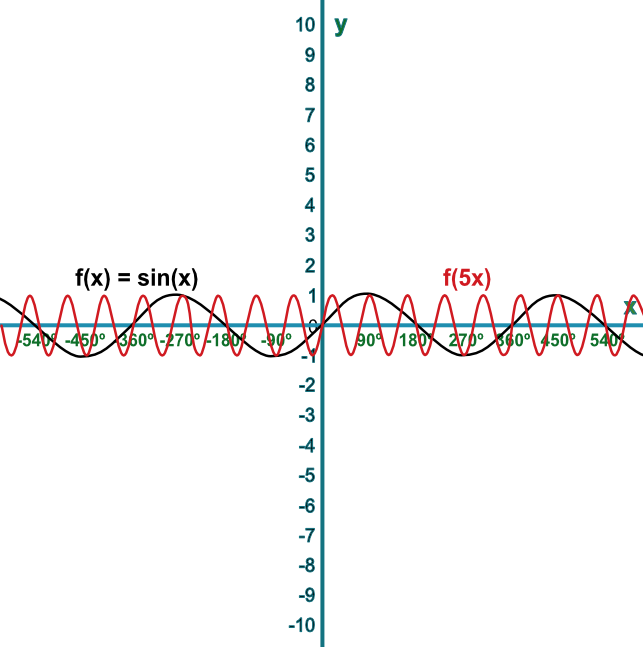
Sketch the graph of the function `f(x)=sin(x)`. On the same graph, sketch `f(5x)`.
Describe the transformation.
A multiple applied before the function is evaluated will expand by a scale factor of the reciprocal of the multiple along the `x`-axis.
Answer: The curve is enlarged parallel to the `x`-axis with a scale factor of `frac(1)(5)`
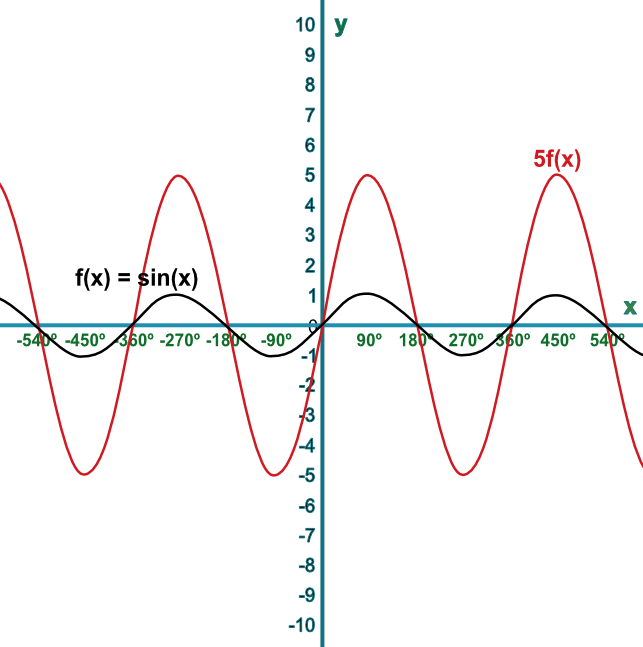
Sketch the graph of the function `f(x)=sin(x)`. On the same graph, sketch `5f(x)`.
Describe the transformation.
A multiple applied after the function is evaluated will expand by a scale factor of the multiple in the direction of the `y`-axis.
Answer: The curve is enlarged parallel to the `y`-axis with a scale factor of 5
See also Expressions as Functions and Enlargement