There are two formulae available for the surface area of a cone. The difference between them is based on whether the slope height or the vertical height is available.
`A = pir^2 + pirl` if the sloping height is known.
`A = pir(r + sqrt(h^2 + r^2))` if the vertical height is known;
The second formula is a variation on the first and incorporates Pythagoras` Theorem into the formulae.
Both formulae include the surface area of the base of the cone.
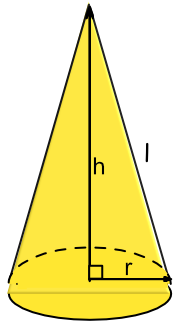
A cone has a radius of 6cm and a vertical height of 12cm. Give the total surface area of the cone to 1 decimal place.
| For a Cone | Area | `= pir(r+sqrt(h^2 + r^2))` |
| Substitute | `A` | `= pi(6)((6)+sqrt((12)^2+(6)^2)` |
| `= pi(6)((6)+sqrt(180)` | ||
| `= 365.99` |
Answer: 366 cm2
A monument based on the shape of the cone is to be covered in metallic paint for an event. Only the sloping surface will be painted. What is the surface area to be covered, if the diameter of the base is 6m and the sloping height of the monument is 12m?
The radius of the base is 3m.
Use `A = pir^2 + pirl`, but only the sloping part of the formula is needed as `pir^2` refers to the base part.
Substituting, `A = pi(3)(12) = 113.097m^2`
Answer: 113m2