Vectors are quantities that have both a magnitude and a direction.
Write the vector in a column, with the movement in the `x`-direction being the top number and the movement in the `y`-direction being the bottom number.
A vector `((5),(7))` gives a displacement in the positive `x` direction, and 7 in the `y` direction.
Vectors are written in a number of ways.
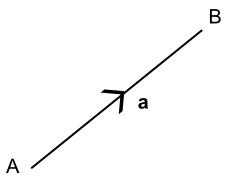
The vector may be written to indicate the start and end points: `vec(AB)`. Direction is important: the vector is going from A to B.
The vector can also be shown as a single letter: this is printed as a (bold a). When writing by hand, underline the letter: `ul(a)`.
Note that these all describe the same vector:
`vec(AB) = ul(a) = `a
A vector that is equal to another vector has the same magnitude and direction, although they may not necessarily be from the same location.
Vector `vec(BA)` is a vector going from B to A. Because it is going in the opposite direction, it is the negative of the original vector.
Vector `vec(AB) = -vec(BA)`
Or using the other syntax:
If vector `vec(AB)` = a and `vec(BA)` = b, then
a = - b
A vector is defined as `vec(AB) = ((3),(4))`. A second vector is defined as `vec(CD) = ((7),(4))`.
Does the vector `vec(AB)` move the same amount in the `y` direction as `-vec(CD)`?
The negative in front of the vector makes the `x` and `y` movements opposite.
Answer: No, as `vec(AB)` moves 4 in the `y`-direction. `-vec(CD)` moves -4 in the `y`-direction as it takes the negative value of the vector.
Vector a is defined as `((-3),(-4))`. Vector b is defined as `((4),(3))`. Does a = -b?
When answering a yes/no question, always provide a valid reason.
Answer: No; neither the `x`-displacement nor the `y`-displacement are equal and opposite.