The volume of a cone is:
`V=pir^2frac(h)(3)`
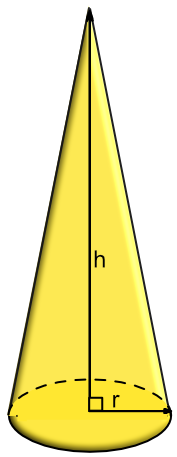
NOTE that `h` is the vertical height of the cone.
A way of remembering this is `frac(1)(3) xx text(vertical height ) xx text( base area)`
A cone has a vertical height of 12cm and a radius of 5 cm. What is the volume of the cone, to 3 significant figures?
| For a cone: | Volume | `= pir^2frac(h)(3` |
| Substitute | `= pi(5)^2 xx frac(12)(3)` | |
| `=314` |
Answer: 314 cm3
The shape shown below consists of a hemisphere placed on a cone. The total volume of the shape is 25 cm3. The overall width of the shape is `x` cm, and the total vertical height of the shape is `3x` cm.
What is the value of `x`? Give your answer to 1 decimal place.

The radius of the hemisphere is `frac(x)(2)`.
The vertical height of the cone is the height of the shape minus the radius, or `3x - frac(x)(2)`
| Hemisphere: | Volume | `= frac(1)(2) xx frac(4)(3)pir^3` |
| `V_h` | `= frac(1)(6) xx frac(4)(3)pifrac(x)(2)^3` | |
| `= frac(1)(12)pix^3` | ||
| Cone: | Volume | `= pir^2h` |
| `V_c` | `= pifrac(x)(2)^2(3x - frac(x)(2))` | |
| `= pifrac(x)(2)^2(frac(6)(2)x - frac(x)(2))` | ||
| `= pifrac(5)(8)x^3` | ||
| Total | `= V_h + V_c` | |
| `25` | `= frac(1)(12)pix^3 + pifrac(5)(8)x^3` | |
| `25` | `= frac(17)(24)pix^3` | |
| `110.8797` | `= x^3` | |
| `4.804` | `= x` |
Answer: 4.8 cm