All straight lines can be written as `y = mx + c`, where the `m` and `c` are numbers.
The `m` gives you the slope, or gradient of the line.
Gradients can be positive or negative. A line rising from left to right is a positive gradient. A line falling from left to right gives a negative gradient.
Up and along can each be negative. Moving bottom to top is positive, and left to right is positive.
The `c` gives the intercept on the y-axis ie when `x = 0`.
What is the gradient and intercept of the line y = -4x - 3?
From `y = mx + c`, `m` = -4 and `c` = -3.
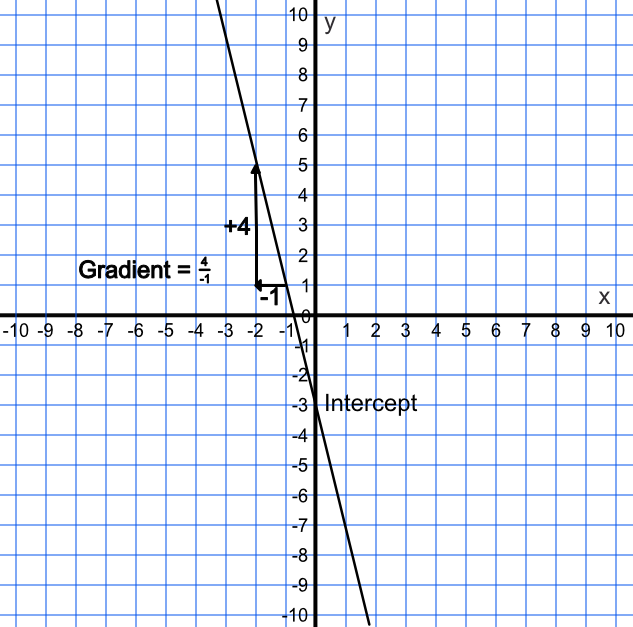
Answer: The gradient is -4; the intercept is -3
Two points on a line are (0, 4) and (1, 7). What is the equation of the line?
It moves along 1 (from 0 to 1).
The line moves up 3 (from 4 to 7).
The gradient is `frac(3)(1)`: `m` = 3
Write the equation as `y = 3x + c`
When `x` = 0, `y = 4`
`4 = 3 xx 0 + c` therefore `c` = 4
`y = 3x + 4`
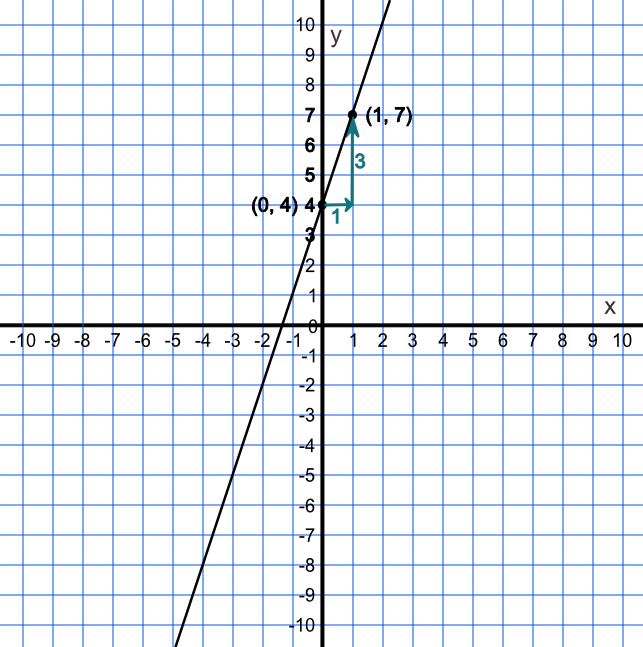
Answer: y = 3x + 4