A quadrilateral where all four vertices touch the circumference of a circle is known as a cyclic quadrilateral.
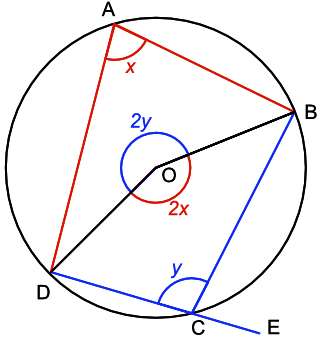
The angle at the centre of a circle is twice that of an angle at the circumference when subtended by the same arc. For arc D-A-B, let the angles be 2`x` and `x` respectively.
For the arc D-C-B, let the angles be 2`y` and `y`.
At the centre of the circle, `360 = 2(x +y), text(or) 180 = x + y`
Opposite angles in a cyclic quadrilateral add up to 180º.
The exterior angle, ∠BCE, is 180 - `y` = `x`.
The exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
What is the value of the angle ∠DAB?
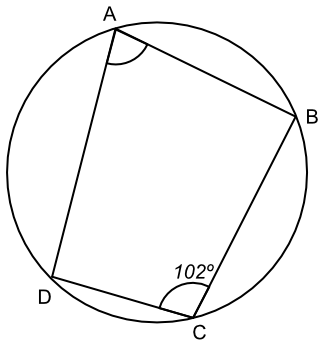
Opposite angles in a quadrilateral add up to 180º.
180 - 102 = 78º
Answer: 78º
Angle ∠ECB is 79º. What is the value of the angle ∠DAB?
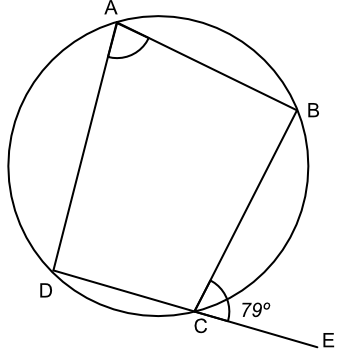
The exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
Answer: 79º
See also Circle Theorems - Subtended Angles