With a curved graph the gradient changes continuously. The gradient gives the rate of change of the item being measured. For kinematic (speed) graphs, the rate of change on a distance-time graph gives velocity. On a velocity-time graph, the rate of change gives acceleration.
To estimate the gradient of a curved line, draw the graph accurately. Then draw a tangent to the graph at the point at which the gradient is required.
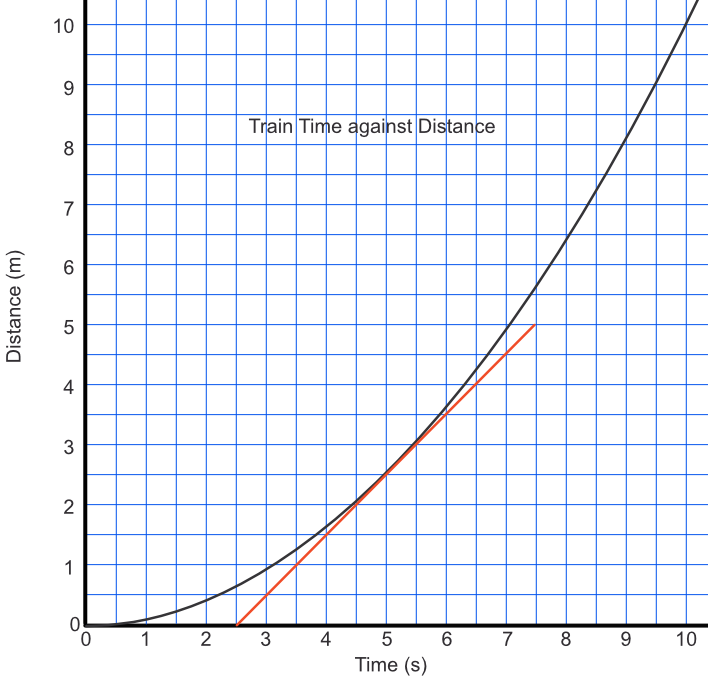
A train moves away from a station with an acceleration of 0.2 ms-2. By drawing a graph of time against distance, estimate the speed of the train after 5 seconds.
The distance travelled by the train is given by `s = frac(1)(2)at^2`, where s is distance, t is time and a is acceleration.
The velocity of the train is given by the gradient of the graph at the point in time in question.
Take the tangent to the graph at x = 5. Extend the line to measure a reasonable gradient. Gradient measures as `frac(5-0)(7.5-2.5) = frac(5)(5) = 1`.
| time (s) | 0 | 2 | 4 | 6 | 8 | 10 |
| dist (m) | 0 | 0.4 | 1.6 | 3.6 | 6.4 | 10 |
Answer: 1 m/s
Using the graph, above, indicate whether the speed of the train is faster at 2 seconds or at 8 seconds.
The gradient of the curve is steeper at 8 seconds compared to the gradient at 2 seconds: the train is therefore moving more quickly.
Answer: Faster at 8 seconds
See also y=mx+c and Gradients and Intercepts of Linear Functions