A gradient for a graph gives the rate of change of the item being measured.
The area under a graph gives the amount consumed over an interval.
If the measurement is distance, then the rate of change of distance is velocity.
If the measurement is velocity, then the rate of change gives acceleration and the area gives the distance.
The graph shows the performance of two similar engines. One runs at a higher rate of rpm (revolutions per minute) than the other. Which engine configuration has the higher rate of acceleration at 5 seconds?
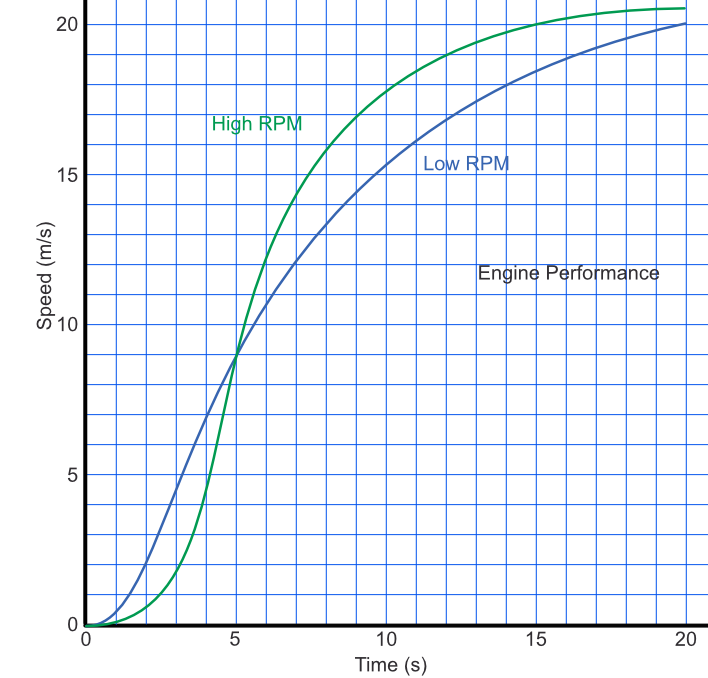
At 5 seconds, the gradient for High RPM is steeper, therefore the acceleration is higher.
Answer: High RPM
At 15 seconds, which engine is giving the higher acceleration?
Although the High RPM has a faster velocity (higher up on the graph), the gradient of the Low RPM engine is steeper. On a velocity-time graph, the gradient gives the acceleration.
Answer: Low RPM
See also Gradients of Graphs as Rates of Change and Velocity