On a distance-time graph, the gradient of the graph gives the velocity of the object being measured:
velocity = `frac(text(distance))(text(time))`
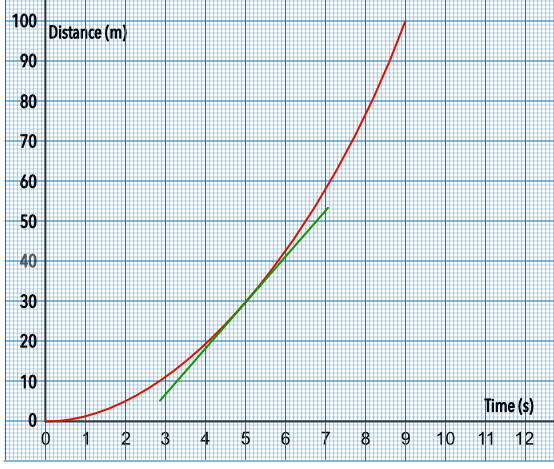
From the distance-time graph, above, what is the velocity of the car at 5 seconds? Give your answer correct to 1 decimal place.
The velocity is the gradient = `frac(text(change in distance))(text(change in time))`
Take a tangent at 5 seconds
Gradient of tangent
= `frac(52.5 - 37)(7 - 3)`
= 3.875 ms-1
Answer: 3.9 ms-1
Using the graph, what is the average velocity for the first 100m? Give your answer correct to 1 decimal place.
Distance covered in 100m took 9 seconds
= `frac(100)(9)`
= 11.11 ms-1
Answer: 11.1 ms-1
See also Kinematic Graphs