If a circle has a radius with centre at the origin, then a point on the circle can be described as being at a point (x, y). The gradient of the line to that point is `frac(y)(x)`.
A line perpendicular to that radius is given by `frac(-1)(text(gradient))` (see perpendicular lines). If the original gradient is `frac(y)(x)`, then the gradient of the perpendicular line is `frac(-x)(y)`.
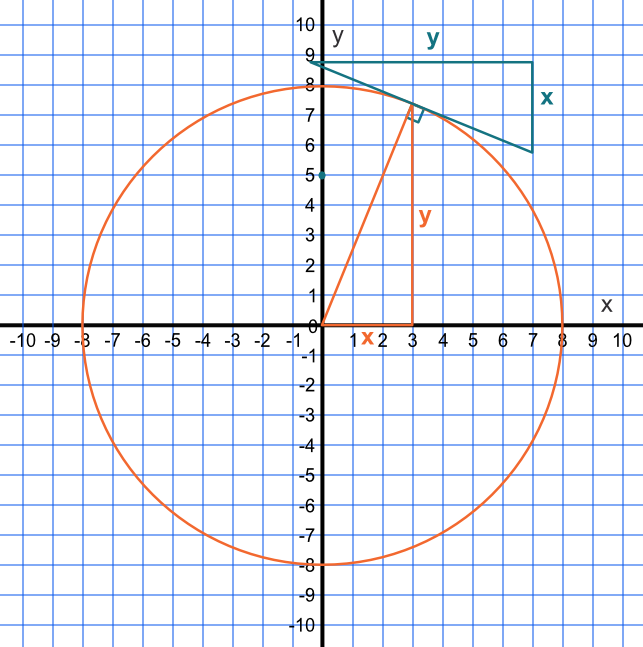
A circular function, centred on the origin, has a radius of 5.
What is the gradient of the tangent to the circle when x = 4?
The y-coordinate can be found by solving `r^2 = x^2 + y^2`
substituting `5^2 = 4^2 + y^2`
`25 = 16 + y^2`, giving `y = 3`
The gradient of the radius at (4, 3) is `frac(3)(4)`. Use the inverse of gradient, and multiply by -1: the tangent is -`frac(4)(3)`.
Answer: -`frac(4)(3)`
The gradient of a tangent to a circle is -`frac(7)(4)`. The circle is centred on the origin. If the radius of the circle is `sqrt(585)`, what are the coordinates of the tangent?
Gradient of the radius to the tangent is the negative inverse of -`frac(7)(4)` = `frac(4)(7)`. The radius of a circle is given by `r^2 = x^2 + y^2`
In this instance the radius is a multiple:
`(mx)^2 + (my)^2 = (mr)^2`
`(7m)^2 + (4m)^2 = (sqrt(585))^2`
`49m^2 + 16m^2 = 585`
`65m^2 = 585`, therefore `m = 3`
The tangent is therefore at (3 x 7, 3 x 4) = (21, 12)
Answer: (21, 12)
See also Perpendicular Lines and Circle Theorems - Tangents